Hvis man skal lave nogle beregninger på en kompliceret funktion, kan det nogle gange være en fordel, hvis man kan finde et simplere udtryk for det udsnit af funktionen, som man skal bruge. Her kan man eksempelvis anvende et Taylor-polynomium.
Hvis vi har en funktion, \(f(x)\), kan vi approksimere funktionen i punktet \(a\) således:
\begin{equation} P_n = f(a) + \frac{f'(a)}{1!}(x - a)^1 + \frac{f''(a)}{2!}(x - a)^2 + \ldots + \frac{f^{(n)}(a)}{n!}(x - a)^n \end{equation}Her kaldes \(P_n\) et Taylor-polynomium af grad \(n\). Vi kan f.eks. lave en Taylor-udvikling af sinus omkring \(a = 0\) til 3. grad:
\begin{align} P_3 &= \sin(0) + \frac{\cos(0)}{1!}(x - 0)^1 - \frac{\sin(0)}{2!}(x - 0)^2 - \frac{\cos(0)}{3!}(x - 0)^3 \\ P_3 &= x - \frac{1}{6}x^3 \end{align}Taylor-polynomiet ser således ud sammenlignet med sinus-funktionen:
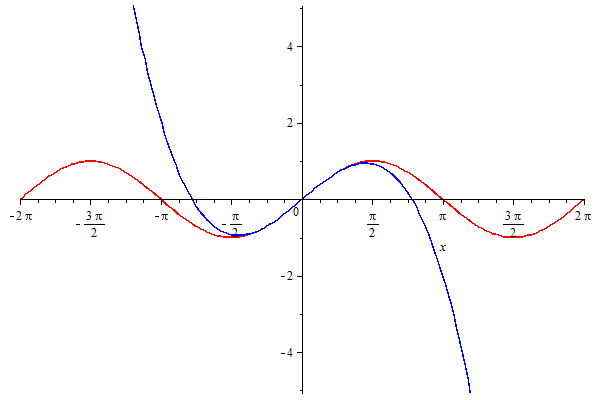
Som det fremgår, passer polynomiet ret godt omkring \(x = 0\), men jo længere væk fra det punkt vi kommer, jo dårligere vil Taylor-polynomiet passe. Desuden kan vi hele tiden forbedre vores approksimation, ved simpelthen blot at tage flere led med - her ses en 14.-grads Taylor-udvikling af sinus omkring \(x = 0\):
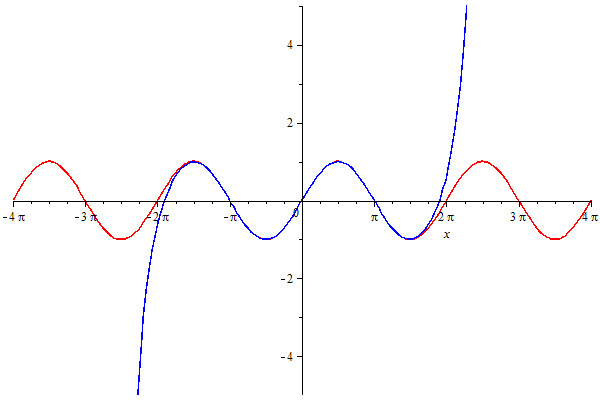
Selvom det oftest er nemmest at Taylor-udvikle en funktion omkring \(x = 0\), kan vi sagtens gøre det omkring et andet punkt i stedet - lad os beregne et 3.-grads Taylor-polynomium af \(\cos(x)\) omkring \(x = \pi/2\):
\begin{align} P_3 &= \cos(\pi/2) - \frac{\sin(\pi/2)}{1!}(x - \pi/2)^1 - \frac{\cos(\pi/2)}{2!}(x - \pi/2)^2 + \frac{\sin(\pi/2)}{3!}(x - \pi/2)^3 \\ P_3 &= -x + \pi/2 + \frac{1}{6}(x - \pi/2)^3 \end{align}Hvilket ser således ud når man tegner det:
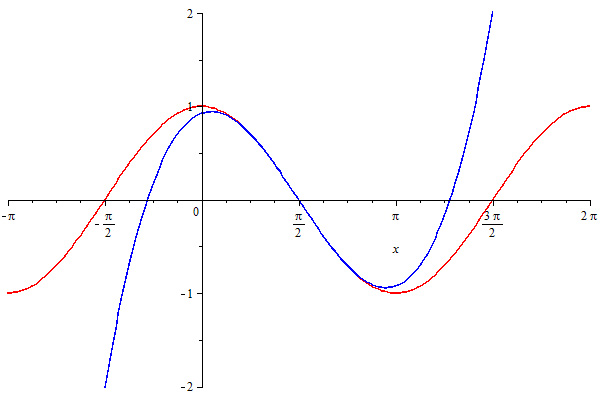
Bemærk, at hvis man laver en Taylor-udvikling af et polynomium, til samme grad som polynomiet, vil Taylor-polynomiet bare blive lig dette polynomium.