Hvad er Komplekse Tal
For at forstå, hvad komplekse tal er, vil vi først se på hvilke forskellige slags tal vi kender i forvejen. Først og fremmest har vi jo de naturlige tal, mængden \(\mathbb{N}\), som er alle positive heltal. Og vi kan jo så spørge os selv - behøver vi flere tal?
Så længe vi bare vil lægge/gange tal sammen, er svaret nej, men hvis vi f.eks. skal løse ligningen \(x + 6 = 4\) får vi et problem - det kan jo ikke lade sig gøre, så længe \(x\in \mathbb{N}\) (altså "\(x\) tilhører \(\mathbb{N}\)")!
Hvis vi i stedet for de naturlige tal, \(\mathbb{N}\), anvender de hele tal, mængden \(\mathbb{Z}\), som er alle positive og negative heltal (inklusiv \(0\)), kan vi løse ligningen (idet \(x = -2\)). Igen kan vi spørge os selv, om vi nu behøver flere tal? Og det gør vi, hvis vi får en ligning som f.eks. \(2x = 1\), da denne ligning ikke kan løses når \(x \in \mathbb{Z}\)! Igen må vi udvide vores talmængde for at løse ligningen - denne gang til de rationale tal, mængden \(\mathbb{Q}\), som også omfatter alle brøker med heltal i både tælleren og nævneren. Og selvom vi nu kan se, at svaret på ligningen er \(x = 1/2\), så får vi bare et nyt problem med ligningen \(x^2 = 2\), fordi \(\sqrt{2}\) (som er løsningen), ikke ligger i de rationale tal - dette tal kan ikke skrives som en brøk af heltal! Derfor udvider vi endnu en gang vores talmængde til de reelle tal, mængden \(\mathbb{R}\), som er den talmængde vi er vant til at regne med.
Og denne gang virker det mere relevant at spørge sig selv, om vi behøver flere tal? Hvis man svarer nej, så får man et problem med følgende ligning:
\begin{equation} x^2 = -1 \end{equation}Som man hurtigt opdager, kan denne ligning ikke løses med reelle tal (man kan ikke tage kvadratroden til et negativt tal), og derfor kommer de komplekse tal, mængden \(\mathbb{C}\), til undsætning! Faktisk må vi stadig ikke tage kvadratroden til et negativt tal, når vi anvender komplekse tal, med ved at definere den imaginære enhed \(i\), således, kan vi komme ud over dette problem:
\begin{equation} i^2 = -1 \end{equation}Vi kan nu anvende denne definition til at løse ligningen ovenfor:
\begin{equation} x^2 = -1 = i^2 \quad \Rightarrow \quad x = \pm\sqrt{i^2} = \pm i \end{equation}På denne måde kunne vi løse ligningen, helt uden at tage kvadratroden til et negativt tal. Bemærk at vi ikke skriver \(i\) op som \(\sqrt{-1}\), men blot lader \(i\) være en del af det komplekse tal, dvs. komplekse tal skrives på formen:
\begin{equation} z = a + i \cdot b \qquad z \in \mathbb{C} \end{equation}Hvor \(a,b \in \mathbb{R}\). Her kaldes \(a\) for realdelen af tallet, mens \(b\) kaldes imaginærdelen af tallet. Bemærk desuden, at hvis \(b = 0\) har vi blot et almindeligt reelt tal tilbage.
Regning med Komplekse Tal
Hvis man er god til simpel algebra, er regning med komplekse tal ingen udfordring - man behandler den imaginære enhed, \(i\), ligesom man ville behandle enhver ubekendt i et matematisk udtryk! Dette fremgår let af, hvordan to komplekse tal lægges sammen. Hvis \(z = a_1 + ia_2\) og \(w = b_1 + ib_2\) får vi:
\begin{equation} z + w = a_1 + ia_2 + b_1 + ib_2 = a_1 + b_1 + i(a_2 + b_2) \end{equation}Og vi kan naturligvis også gange to komplekse tal sammen:
\begin{align} zw &= (a_1 + ia_2)(b_1 + ib_2) \\ &= a_1b_1 + i^2a_2b_2 + i(a_1b_2 + a_2b_1) \\ &= a_1b_1 - a_2b_2 + i(a_1b_2 + a_2b_1) \end{align}Altså bliver \(a_1b_1 - a_2b_2\) vores realdel, og \(a_1b_2 + a_2b_1\) imaginærdelen. Lad os se et eksempel, hvor \(z = 2i\) og \(w = 1 - i\):
\begin{align} z + w &= 2i + 1 - i = 1 + i \\ zw &= 2i(1 - i) = - 2i^2 + 2i = 2 + 2i \end{align}Man kan naturligvis også dividere tallene:
\begin{equation} \frac{w}{z} = \frac{1 - i}{2i} = \frac{1}{2i} - \frac{1}{2} = -\frac{1}{2}i - \frac{1}{2} \end{equation}Her har vi benyttet følgende egenskab ved den imaginære enhed:
\begin{equation} i^2 = -1 \quad \Rightarrow \quad i = -\frac{1}{i} \end{equation}Man kan altså regne med komplekse tal vha. ganske almindelig algebra.
Det Komplekse Plan og Polærform
Vi er vant til, at vi kan afsætte tal på en tallinie, men for komplekse tal er det anderledes - nu har vi to tallinier (en for realdelen og en for imaginærdelen), som står vinkelret på hinanden, således at de danner et komplekst plan. Her ses en række tal afsat på det komplekse plan:
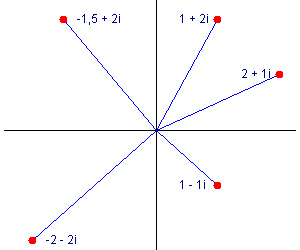
Førsteaksen kaldes den reelle akse og andenaksen den imaginære akse. Vi kan desuden se ud fra dette, at komplekse tal minder meget om vektorere i planen.
Ud fra dette kan vi desuden også se, at et komplekst tal kan beskrives vha. en vinkel og en længde, dvs. på formen:
\begin{equation} z = r(\cos(\theta) + i\sin(\theta)) \end{equation}Denne form kaldes polærformen for et komplekst tal, og længden \(r\) kaldes modulus af tallet mens vinklen \(\theta\) kaldes tallets argument.
Vi finder modulus af et tal ved at gange tallet med sin komplekst konjugerede, og dernæst tage kvadratroden. Den komplekst konjugerede til et tal, er blot det samme tal med modsat fortegn på imaginærdelen - dette svarer til at spejle tallet i den reelle akse i det komplekse plan (bemærk desuden, at den komplekst konjugerede til et reelt tal er tallet selv). Har vi f.eks. \(z = 1 - i\) er den komplekst konjugerede \(\overline{z} = 1 + i\) og modulus, \(|z|\), bliver derfor:
\begin{equation} |z| = \sqrt{z\overline{z}} = \sqrt{(1 - i)(1 + i)} = \sqrt{1^2 - i^2} = \sqrt{2} \end{equation}Når vi skal finde argumentet, \(arg(z)\) eller blot \(\theta\), kan vi anvende simpel trigonometri (idet real- og imaginærdelen af tallet udgør to kateter i en retvinklet trekant, i det komplekse plan):
\begin{equation} \tan(\theta) = \frac{\text{Im}(z)}{\text{Re}(z)} \end{equation}Her angiver \(\text{Im}(z)\) imaginærdelen af \(z\) (uden at skrive \(i\) med) og \(\text{Re}(z)\) angiver realdelen. Bemærk desuden, at argumentet altid er vinklen mellem tallet og den positive del af den reelle akse, som det fremgår her, hvor argumentet er vist for en række tal:
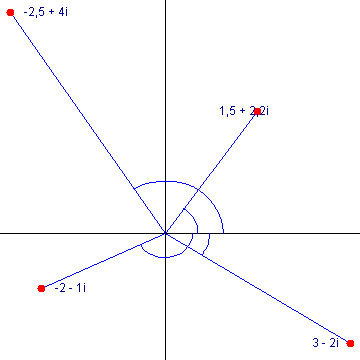
Argumentet, \(arg(z)\) kan have en hvilken somhelst værdi, men vi kan også definere hovedargumentet, der er argumentet givet ved \(\text{Arg}(z) \in \{-\pi \leq \arg(z) \leq \pi\}\), dvs. argumentet opgivet i intervallet \(\pm\pi\) (bemærk at hovedargumentet skrives med stort A, altså \(\text{Arg}(z)\)).
Lad os tage et eksempel med \(z = 2 + 2i\). Vi finder modulus og argument, hvorefter vi kan opskrive tallet på polærform:
\begin{align} |z| &= \sqrt{(2 + 2i)(2 - 2i)} = \sqrt{2^2 + 2^2} = \sqrt{8} \\ \theta &= \tan^{-1}\left(\frac{2}{2}\right) = \frac{\pi}{4} \\ z &= \sqrt{8}\cdot(\cos(\pi/4) + i\sin(\pi/4)) \end{align}Det kan, som vi skal se, nogle gange være en fordel at have et komplekst tal på polærform, frem for den normale, kartesiske form.
Den Komplekse Eksponentialfunktion
Når vi snakker komplekse tal, er eksponentialfunktionen meget vigtig. Den er for et komplekst tal, \(z = a + ib\), givet således:
\begin{equation} e^z = e^{a + ib} = e^a e^{ib} = e^a (\cos(b) + i\sin(b)) \end{equation}Heraf kan vi altså se, at \(|e^z| = e^{\text{Re}(z)}\) samt \(\arg(e^z) = \text{Im}(z)\). Dvs. hvis realdelen er \(0\), har vi \(|e^z| = 1\), hvoraf det fremgår, at polærformen for et komplekst tal kan skrives således:
\begin{equation} z = |z|e^{i\theta} \end{equation}Altså en meget nemmere måde at opskrive et tal på! Vi kan desuden opskrive sinus og cosinus som funktion af komplekse eksponentialfunktioner:
\begin{align} \cos(x) &= \frac{e^{ix} + e^{-ix}}{2} \\ \sin(x) &=\frac{e^{ix} - e^{-ix}}{2i} \end{align}Disse ligninger kan bl.a. anvendes til at udlede forskellige regneregler for sinus og cosinus.
De Moivres Sætning
En vigtig sætning der bør nævnes, er de Moivres sætning:
\begin{equation} (\cos(\theta) + i\sin(\theta))^n = \cos(n\theta) + i\sin(n\theta) \qquad \text{eller blot} \qquad (e^{i\theta})^n = e^{in\theta} \end{equation}Dette er altså helt trivielt hvis blot man kan sine potensregneregler, men det er ikke desto mindre en vigtig sætning. Vi kan eksempelvis anvende den til at finde kvadratroden af tallet \(z = 2 + 2i\):
\begin{align} \sqrt{z} &= \sqrt{2 + 2i} = \sqrt{\sqrt{8}e^{i\pi/4}} = 2^{3/4}\left(e^{i\pi/4}\right)^{1/2} \\ &= 2^{3/4}e^{i\pi/8} \approx 1,55 + 0,64\cdot i \end{align}Dette er altså et eksempel på, at polærformen kan være nyttig (og resultatet er desuden pænest i polær form!).
Anvendelser af Komplekse Tal
Nu har vi efterhånden styr på de komplekse tal, men hvad kan vi så bruge dem til? Vi kan f.eks. se på Hookes lov fra fysikken, der siger, at kraften fra en fjeder er givet ved \(F = -kx\). Sætter vi det sammen med Newtons 2. lov får vi følgende differentialligning:
\begin{equation} m\frac{d^2x}{dt^2} = -kx \end{equation}Du har måske allerede lært i fysik, at f.eks. \(\sin(x)\) og \(\cos(x)\) er løsninger til dette system, men generelt når man skal løse 2.-ordens differentialligninger, kræver det komplekse tal. Desuden vil \(e^{z}\) for enhver \(z\in\mathbb{C}\) også være en løsning til ligningen, selvom denne ikke er fysisk mulig (positionen af en fjeder skal være givet ved et reelt tal). Dog vil denne type løsning godt kunne bruges i eksempelvis kvantemekanik (det er faktisk en løsning til Schrödinger-ligningen for en fri partikel, hvis man ikke tager højde for Born-fortolkningen af bølgefunktionen).
For at vise et eksempel på anvendelsen, kan vi udlede en regneregl for cosinus:
\begin{equation} (\cos(x))^2 = \left( \frac{e^{ix} + e^{-ix}}{2} \right)^2 = \frac{e^{i2x} + e^{-i2x} + 2}{4} = \frac{1 + \cos(2x)}{2} \end{equation}På samme måde kan mange andre regneregler udledes.