Begrebet pathfinding dækker over processen i at finde den bedst mulige vej mellem to veldefinerede punkter, A og B. Der er oftest tale om den hurtigste vej, men en lang række faktorer kan spille ind, alt efter i hvilken forbindelse det anvendes. En hurtig algoritme til bestemmelse af den bedst mulige rute gennem et veldefineret område er A*-algoritmen (udtalt ”A-star”), men mange andre algoritmer findes.
Pathfinding kræver som nævnt et veldefineret område, ”søgeområdet”. Vi vil her anvende området vist i Figur 1, som er inddelt i felter for at simplificere processen. Startfeltet, A, er markeret med grøn, mens destinationsfeltet, B, er markeret med blå. De grå felter er blokerede, og en path kan derfor ikke gå gennem dem. Det bør nævnes, at når man beregner en rute/path, kaldes det også for en søgning (idet man søger felterne igennem efter den bedst mulige løsning).
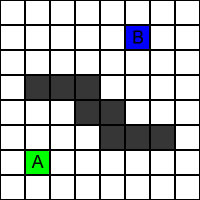
Figur 1 - Område for pathfinding.
Søgningen
Når man laver en søgning vha. A*, anvender man to lister (f.eks. arrays eller kædede lister), kaldet hhv. en åben og en lukket liste. Den åbne liste kommer til at indeholde felter som mangler at blive tjekket, mens den lukkede liste indeholder felter som er blevet tjekket. Felter som er blokerede bliver smidt i den lukkede liste så snart man støder på dem i søgningen, da kun felter som kan indgå i ruten kan tilføjes til den åbne liste.
Ved søgningens start er listerne tomme, og startfeltet, A, tilføjes til den lukkede liste. Derefter køres følgende trin igennem:
- Feltet med den laveste cost i den åbne liste findes.
- For de fire (eller otte, hvis man vil tillade diagonal bevægelse) omkringliggende felter beregnes en cost for hver, hvorefter de tilføjes til den åbne liste. Blokerede felter tilføjes i stedet til den lukkede liste, og cost beregnes ikke for disse.
- Feltet, som fik sine omkringliggende felters cost beregnet, flyttes nu fra den åbne til den lukkede liste.
Disse tre trin itereres indtil et af de omkringliggende felter er målet, felt B, eller til den åbne liste er tom – er det ikke muligt at komme fra A til B vil den åbne liste til sidst blot blive tom. Desuden bør hvert felt indeholde en reference til det foregående felt, for at pathen kan følges ved blot at følge en kædet liste af felter.
Beregning af felters cost
For at beregne den hurtigst mulige path, må man have et mål for hvor hurtig en rute er – til dette anvendes en værdi kaldet cost, og ofte betegnet F. Ruten med den laveste cost, er den hurtigste. Værdien F er summen af to andre værdier:
\begin{equation} F = G + H \end{equation}G-værdien bliver tildelt efter hvor mange felter, man skal gå gennem for at komme hen til det pågældende felt. Tillader man diagonal bevægelse skal man huske, at en diagonal bevægelse er længere end en udelukkende horisontal eller vertikal bevægelse (en diagonal bevægelse er en faktor kvadratrod 2 længere), derfor skal en horisontal eller vertikal bevægelse give +1 i G-værdi, mens en diagonal bevægelse skal give ca. +1,4 i G-værdi. Her skal det dog bemærkes, at computeren er hurtigere til håndtering af heltal end decimaltal, hvorfor det er mere hensigtsmæssigt at anvende værdierne 10 og 14 i stedet. På Figur 2 ses G-værdierne indtegnet på alle felter.
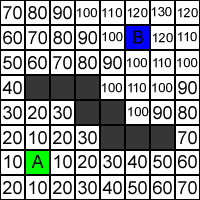
Figur 2 - G-værdier indtegnet uden diagonal bevægelse.
Hvis man kun anvendte G-værdien kunne man sagtens finde den korteste vej, men det ville kræve at den blev beregnet for alle felter – dette ville være alt for ressourcekrævende når først labyrinten blev skaleret op til f.eks. 100x100 felter, hvis flere entiteter i labyrinten skulle lave disse beregninger samtidig (og særligt når algoritmen skal overføres på en 3D-verden).
Derfor anvendes ligeledes en H-værdi (kaldet heuristic), som egentlig blot er et simpelt gæt på hvor langt der er til destinationen. Der findes forskellige måder at beregne en H-værdi på, men jeg har valgt en meget simpel løsning:
\begin{equation} H = (\delta x + \delta y)*10 \end{equation}Hvor \(\delta x\) er differensen i felter langs x-aksen, mens \(\delta y\) er differensen i felter langs y-aksen (altså differensen mellem det pågældende felt, som værdien beregnes for, og destinationsfeltet). Desuden multipliceres med 10, for at få et tal af samme størrelsesorden som G-værdien. Figur 3 viser H-værdien på felterne mellem A og B – men i modsætning til Figur 2 vises dog kun de felter, som vil blive tjekket i søgningen for dette eksempel.
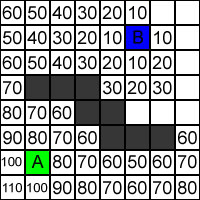
Figur 3 - H-værdier for felter som bliver tjekket i løbet af en søgning.
Felter uden tal ligger for langt væk fra den korteste rute til, at der bruges computerkraft på dem. For at se hvilke felter som bliver tjekket, må F-værdien beregnes. Figur 4 viser F-cost.
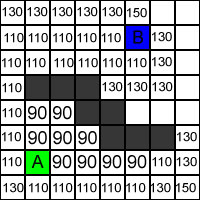
Figur 4 - F-costs.
Efter søgningen
Når søgningen er slut, vil man enten stå med et felt der ligger ved siden af destinationen (hvis der blev fundet en path), eller en path til punktet længst væk fra A, indenfor området (hvis der ikke kunne oprettes en path til destinationen). Sidstnævnte eksempel kan f.eks. ses, hvis punkt A eller B er omringet af blokerede felter.
Idet man til sidst står med feltet ved siden af destinationen (eller selve destinationen, alt efter hvordan det er programmeret), får man altså en path som starter fra destinationspunktet, B, og bevæger sig ad den hurtigste vej til startpunktet, A. Derfor kan det nogle gange være en fordel at starte beregningerne fra destinationspunktet i stedet.